An N-body simulation is simulation of a dynamical system of particles under the influence of physical forces such as gravity.
In a basic N-body simulation every body exerts force on every other body in the system.
This means that in every step of the simulation a net force from all the other bodies has to be computed for each of the bodies before their positions and speeds can be updated.
Such a brute force simulation takes O(n^2) time for each simulation step, where n is the number of particles, so it is not practical for a larger number of bodies.
Instead, we will use a spatial data-structure called a quadtree to determine the relative proximity of the particles and then approximate the impact of many particles that are far apart as if they were a single particle.
This technique is used in the Barnes-Hut simulation, and decreases the computational complexity to O(n logn).
In this larger example of a data-parallel application we will examine the gravitational interaction of clusters of stars. Our simulation might end up looking something like this:

But, how does the afore-mentioned quadtree men help us avoid traversing all the other stars when calculating the net force on a particular star?
The quadtree is a tree data structure where every internal node has exactly four children
(called nw, ne, sw and se).
Every internal node divides a region of 2D space into four quadrants – the elements of each of the four quadrants are recursively
contained in the child nodes.
The leaves of the quadtree represent specific elements.
Here is an example of a quadtree for elements A, B, C and D positioned in a 2D plane:
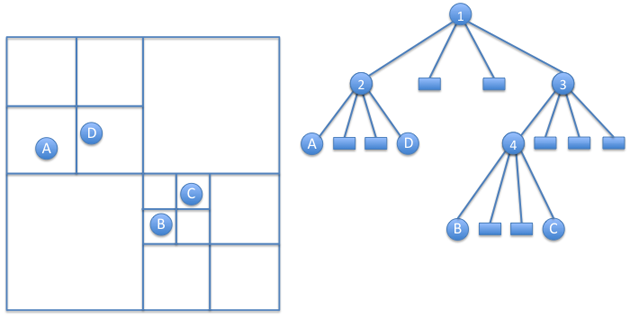
Each internal node divides the rectangle into 4 smaller quadrants, until the quadrant only contains a single element.
The structure of the quadtree altogether contains information about which elements are close to each other.
Nodes B and C share a common parent 4, since they are in the same quadrant represented by the internal node 4.
The Barnes-Hut algorithm is based on the clever idea that many bodies that are sufficiently far away can be approximated
with a single body with their total mass positioned at their center of mass.
In the example above, the force exerted on A from D must be calculated directly, since they are close together,
but the net force on A from bodies B and C can be calculated from the internal node 4 – we only need to store
their total mass and center of mass at node 4.
What is the condition that a bunch of bodies in some quadrant can be approximated with a single body?
In Barnes-Hut simulation criteria commonly used is that an internal node with a center of mass at (xc, yc) can approximate a bunch of bodies
exerting force on a body B positioned at (xb, yb) if and only if the ratio s / d < 0.5, where d is the distance between (xc, yc) and (xb, yb)
and s is the width of the quadrant.
So, for each body B we will traverse the quadtree in-order from the root and update the net force on the body B every time we hit a leaf
or an internal node with the described property (in which case we do not descend the internal node further).
For each body we expect to end up traversing log n nodes of the quadtree, achieving the desired O(n logn) bounds for each if the steps.
To summarize – the Barnes-Hut simulation proceeds in steps, and each step consists of several phases:
- In each step, bounds on all the positions have to be calculated first.
- A quadtree is then constructed based on the positions of all the bodies and their bounds.
- At this point the net force on all the bodies can be calculated by traversing the quadtree for each of the bodies.
- Finally, we remove the bodies that are too far away and unlikely to affect the simulation anymore.
Constructing the quadtree
So lets get started by declaring a quadtree.
We will represent all the nodes of the quad tree with a sealed trait Quad,
armed with some utility methods:
sealed trait Quad {
def massX: Float
def massY: Float
def mass: Float
def total: Int
def update(fromX: Float, fromY: Float, sz: Float, b: Quad.Body): Quad
def distance(fromX: Float, fromY: Float): Float = {
math.sqrt(((fromX - massX) ^ 2) + ((fromY - massY) ^ 2)).toFloat
}
def force(m: Float, dist: Float) = gee * m * mass / (dist * dist)
}
Any node, including leaves, has a certain center of mass.
For single bodies at (x, y) that is the position of the body – massX = x and massY = y.
As for internal nodes, the center of mass can be computed as follows:
val mass = Seq(nw, ne, sw, se).foldLeft(0.0f)(_ + _.mass)
val massX = Seq(nw, ne, sw, se).foldLeft(0.0f) {
(mx, n) => mx + n.massX * n.mass)
} / mass
val massY = Seq(nw, ne, sw, se).foldLeft(0.0f) {
(my, n) => my + n.massY * n.mass
} / mass
In other words, the center of mass is just a weighted average of the centers of mass of the children nodes.
Value total is the total number of bodies in this quadrant.
The utility method distance computes the distance from the position (fromX, fromY) and
the method force computes the force contribution against a body of mass m that is dist distance
units apart.
The model of the force that we chose here is proportional to the masses of the two bodies and
inversely proportional to their square distance, as is the case with the gravitational and electrical force.
Finally, the method update will be used extensively during the quadtree construction phase.
Given the this quadtree which corresponds to a quadrant starting at (fromX, fromY) with width sz,
and a new body b, this method modifies this quadtree and returns a quadtree that contains b.
A Quad will thus be a mutable data structure.
Importantly, note that we pass fromX, fromY and sz as arguments to update because
we will only keep information about the corresponding quadrant size in internal nodes, but not in leaves.
Here is how we will define the empty tree (we only show the relevant methods below):
case object Empty extends Quad {
def massX = 0.0f
def massY = 0.0f
def mass = 0.0f
def total = 0
def update(fromX: Float, fromY: Float, sz: Float, b: Body) = b
}
Updating the empty tree just returns the body b of type Body.
Obviously, we also have to make the type Body extend Quad – to reduce
object allocations we will use bodies as leaves in the tree directly.
The Body nodes represent leaves and they are updated by first creating
an internal node Fork in the corresponding quadrant with Empty children,
and then updating that Fork with this Body and the other Body b.
case class Body(val id: Int)(
val x: Float,
val y: Float,
val xspeed: Float,
val yspeed: Float,
val mass: Float
) extends Quad {
def update(fromX: Float, fromY: Float, sz: Float, b: Body) = {
val centerX = fromX + sz / 2
val centerY = fromY + sz / 2
val fork = new Fork(cx, cy, sz)(Empty, Empty, Empty, Empty)
fork.update(fromX, fromY, sz, this).update(fromX, fromY, sz, b)
}
}
Finally, internal nodes are represented with the type Fork.
The updating works by finding the proper quadrant and updating that child.
case class Fork(val centerX: Float, val centerY: Float, val size: Float)
(var nw: Quad, var ne: Quad, var sw: Quad, var se: Quad)
extends Quad {
var massX: Float = _
var massY: Float = _
var mass: Float = _
def total = nw.total + ne.total + sw.total + se.total
def update(fromx: Float, fromy: Float, sz: Float, b: Body, depth: Int) = {
val hsz = sz / 2
if (b.x <= centerX) {
if (b.y <= centerY) nw = nw.update(fromx, fromy, hsz, b, depth + 1)
else sw = sw.update(fromx, centerY, hsz, b, depth + 1)
} else {
if (b.y <= centerY) ne = ne.update(centerX, fromy, hsz, b, depth + 1)
else se = se.update(centerX, centerY, hsz, b, depth + 1)
}
updateStats()
this
}
}
We already said that Quad will be a mutable data structure.
Since we do not return a new Fork, but update the children of this Fork in place,
we must remember to update the total mass and the center of mass (massX, massY) fields after
updating the quadtree.
This is done in the updateStats() method as follows:
def updateStats() {
mass = nw.mass + sw.mass + ne.mass + se.mass
if (mass > 0.0f) {
massX = (
nw.mass * nw.massX +
sw.mass * sw.massX +
ne.mass * ne.massX +
se.mass * se.massX
) / mass
massY = (
nw.mass * nw.massY +
sw.mass * sw.massY +
ne.mass * ne.massY +
se.mass * se.massY
) / mass
} else {
massX = 0.0f
massY = 0.0f
}
}
And that’s it – our quadtree is implemented. Next, lets see how we can update the positions and speeds of the bodies using the quadtree.
Updating the bodies
We will now add another method to our Body type that will, given the current body and a quadtree,
compute the net force on the current body and use that to return a new body with the updated position and speed.
We call this method updatePosition:
def updatePosition(quad: Quad, delta: Float, theta: Float): Body = {
var netforcex = 0.0f
var netforcey = 0.0f
We start by defining accumulators for the x and y components of the net force.
We the define a recursive method traverse to traverse the quad tree and
update the net force as needed:
def traverse(quad: Quad): Unit = quad match {
case Empty =>
// no force
case _ =>
val dist = quad.distance(x, y)
quad match {
case f @ Fork(cx, cy, sz) if f.size / dist >= theta =>
traverse(f.nw)
traverse(f.sw)
traverse(f.ne)
traverse(f.se)
case Body(thatid) if id == thatid =>
// skip self
case _ =>
val dforce = quad.force(mass, dist)
val xn = (quad.massX - x) / dist
val yn = (quad.massY - y) / dist
val dforcex = dforce * xn
val dforcey = dforce * yn
netforcex += dforcex
netforcey += dforcey
}
}
traverse(quad)
If the node contains no bodies (Empty), then the traverse method does not update the net force.
Otherwise, if the current node is an internal node f such that f.size / dist is bigger than or equal to the threshold theta (by default 0.5),
then the internal node is too close to the body, and we have to add the force contributions by traversing its subquadrants.
If the quadtree node is the same body as the body being updated, then we skip it – a body does not exert force on itself.
Finally, in all other cases (another body or a quadrant of bodies sufficiently far away) we compute the force contribution (dforcex, dforcey)
in the direction of the normal vector (xn, yn) from the current body to the target body/quadrant.
We then add (dforcex, dforcey) to the net force.
After the net force has been computed, we proceed by computing the new position and speed of the current body.
In doing so, we use a parameter delta that can be tuned to control the precision of the simulation:
val nx = x + xspeed * delta
val ny = y + yspeed * delta
val nxspeed = xspeed + netforcex / mass * delta
val nyspeed = yspeed + netforcey / mass * delta
new Body(id)(nx, ny, nxspeed, nyspeed, mass)
}
Finally, we return the new body.
Eliminating outliers
During the Barnes-Hut simulation some of the bodies occasionally become distanced from the other bodies and achieve velocity such that they will never again come into the proximity of the rest of the bodies. We can safely eliminate such bodies from the simulation, as they are no longer relevant. The condition we will use to detect such bodies will be that they are sufficiently far away from the center of mass of all the bodies, and that their relative speed in the direction away from the center of mass is greater than the escape velocity.
def isOutlier(b: Body, quadtree: Quad) {
val dx = quadtree.massX - b.x
val dy = quadtree.massY - b.y
val d = math.sqrt(dx * dx + dy * dy)
if (d > eliminationThreshold) {
val nx = dx / d
val ny = dy / d
val relativeSpeed = b.xspeed * nx + b.yspeed * ny
if (relativeSpeed < 0) {
val escapeSpeed = math.sqrt(2 * gee * quadtree.mass / d)
if (-relativeSpeed > 2 * escapeSpeed) outliers += b
}
}
}
Parallelizing the simulation
We can now try to parallelize each of the simulation separately.
First, we need to find the boundaries of a rectangle in which we can place all the bodies currently being simulated. Bodies change their positions in each step, so this rectangle continually changes.
Boundaries consist of four different values – minimum x and maximum x coordinates, and minimum y and maximum y coordinates.
We represent this with a class Boundaries:
class Boundaries extends Accumulator[Body, Boundaries] {
var minX = Float.MaxValue
var minY = Float.MaxValue
var maxX = Float.MinValue
var maxY = Float.MinValue
def size = math.max(maxX - minX, maxY - minY)
}
This class is a subclass of the Accumulator trait.
Accumulators are special kind of Mergers – the only difference is that they do not return some parallel collection
as a result, but instead return themselves as results.
The fact that accumulators are mergers means that they must implement several important methods,
namely, merge, += and clear.
These are easy:
def +=(b: Quad.Body) = {
minX = math.min(b.x, minX)
minY = math.min(b.y, minY)
maxX = math.max(b.x, maxX)
maxY = math.max(b.y, maxY)
this
}
def clear() {
minX = Float.MaxValue
minY = Float.MaxValue
maxX = Float.MinValue
maxY = Float.MinValue
}
def merge(that: Boundaries) = if (this eq that) this else {
val res = new Boundaries
res.minX = math.min(this.minX, that.minX)
res.minY = math.min(this.minY, that.minY)
res.maxX = math.max(this.maxX, that.maxX)
res.maxY = math.max(this.maxY, that.maxY)
res
}
The reason why we want to have an accumulator for the boundaries is that we can use the accumulate method with it.
This method will in parallel construct several Boundaries objects, add all the bodies into them using += and then
merge these Boundaries objects together.
Accumulators are much more efficient than maintaing an immutable quadruple of bounds and using the aggregate operation on this quadruple.
val boundaries = bodies.toPar.accumulate(new Boundaries)
At this point we can construct the quad tree in parallel.
Constructing the quad tree would potentially require updating its root, so multiple threads cannot do it in parallel without synchronization.
So, lets instead create another accumulator called Sectors.
This accumulator divides the boundaries into which all the bodies can be placed into 2^N x 2^N identical rectangles, and constructs the quad tree separately in each of those sectors.
For example, in the figure at the beginning we have 2x2 sectors – only sectors corresponding to nodes 2 and 3 contain objects [A, D] and [B, C], respectively.
The Sectors accumulator will use += to group bodies into 2^N x 2^N buckets depending on which rectangle they belong to.
When merging, they will merge their corresponding buckets:
class Sectors(val boundaries: Boundaries)
extends Accumulator[Body, Sectors] {
var buckets = Array.fill(twoToN * twoToN)(new Conc.Buffer[Body])
val sectorSize = boundaries.size / twoToN
def clear() {
buckets = Array.fill(twoToN * twoToN)(new Conc.Buffer[Body])
}
def +=(b: Body) = {
val sx = math.min(
twoToN - 1,
((b.x - boundaries.minX) / sectorSize).toInt)
val sy = math.min(
twoToN - 1,
((b.y - boundaries.minY) / sectorSize).toInt)
buckets(sy * twoToN + sx) += b
this
}
def merge(that: Sectors) = {
val res = new Sectors(boundaries)(comb)(op)
for (x <- 0 until twoToN; y <- 0 until twoToN) {
val idx = y * twoToN + x
res.buckets(idx) = this.buckets(idx) merge that.buckets(idx)
}
res
}
}
Above, each bucket in the array of 2^N x 2^N buckets is represented with a Conc buffer.
Conc buffers are an extremely fast append-at-the-end buffers that can be efficiently merged
with their own merge operation in logarithmic time.
Once we obtain the list of all the bodies grouped into buckets corresponding to different sectors,
we can create a quad tree for each of them.
We add a method toQuad to the Sectors class:
def toQuad: Quad = {
val quads = for ((bs, idx) <- sectors.buckets.zipWithIndex.toPar) yield {
val sx = idx % twoToN
val sy = idx / twoToN
val sectorSize = boundaries.size / twoToN
var quad: Quad = Quad.Empty
val fromX = boundaries.minX + sx * sectorSize
val fromY = boundaries.minY + sy * sectorSize
for (b <- bs.result) {
quad = quad.update(fromX, fromY, sectorSize, b)
}
}
mergeQuads(quads)
}
The mergeQuads method then merges all the quads by adding additional nodes that connect them.
We do not show it here, but you can take a look at the source code to see how that part works.
Once we have the quad tree, we must compute the net force on each of the bodies,
and update their speeds and positions.
Since we already have the updatePosition method, this is easy.
We simply map each body into a new body in parallel:
val newBodies = for (b <- bodies.toPar) yield
b.updatePosition(quad, delta, theta)
As the final phase of the simulation phase, we need to filter out bodies that are escaping the simulation.
Again, this is just a parallel filter operation:
bodies = newBodies.filter(isOutlier(_, quad))
You can see the complete code for the parallel Barnes-Hut simulation here. If your browser supports Java, you can also run the applet below directly to see the simulation right away.
